Continuous Algebraic Riccati Equation of 2 States Example

Open access

Optimal Solution to Matrix Riccati Equation – For Kalman Filter Implementation

Submitted: December 5th, 2011 Published: September 26th, 2012

DOI: 10.5772/46456

From the Edited Volume

MATLAB

Edited by Vasilios N. Katsikis

IntechOpen Downloads

14,407

Total Chapter Downloads on intechopen.com

Altmetric score

Overall attention for this chapters

• Bhar K. Aliyu

• Charles A. Osheku

• Lanre M.A. Adetoro

• Aliyu A. Funmilayo

*Address all correspondence to:

1. Introduction

Matrix Riccati Equations arise frequently in applied mathematics, science, and engineering problems. These nonlinear matrix equations are particularly significant in optimal control, filtering, and estimation problems. Essentially, solving a Riccati equation is a central issue in optimal control theory. The needs for such equations are common in the analysis and synthesis of Linear Quadratic Gaussian (LQC) control problems. In one form or the other, Riccati Equations play significant roles in optimal control of multivariable and large-scale systems, scattering theory, estimation, and detection processes. In addition, closed forms solution of Riccti Equations are intractable for two reasons namely; one, they are nonlinear and two, are in matrix forms. In the past, a number of unconventional numerical methods were employed for the solutions of time-invariant Riccati Differential Equations (RDEs). Despite their peculiar structure, no unconventional methods suitable for time-varying RDEs have been constructed, except for carefully re-designed conventional linear multistep and Runge-Kutta(RK) methods.

Implicit conventional methods that are preferred to explicit ones for stiff systems are premised on the solutions of nonlinear systems of equations with higher dimensions than the original problems via Runge-Kutta methods. Such procedural techniques do not only pose implementation difficulties but are also very expensive because they require solving robust non-linear matrix equations.

In this Chapter, we shall focus our attention on the numerical solution of Riccati Differential Equations (RDEs) for computer-aided control systems design using the numerical algorithm with an adaptive step of Dormand-Prince . It is a key step in many computational methods for model reduction, filtering, and controller design for linear systems. In the meantime, we shall limit our investigation to the optimality in the numeric solution to Riccati equation as it affects the design of Kalman-Bucy filter state estimator, for an LQG control of an Expendable Launch Vehicle (ELV) in pitch plane during atmospheric ascent. Furthermore, the approach in the paper by Aliyu Kisabo Bhar et al will be fully employed from a comparative standpoint of the solution to a differential Riccati equation and an Algebraic Riccati for Kalman-Bucy filter implementation.

Advertisement

2. Kalman filter

Theoretically the Kalman Filter is an estimator for the linear-quadratic problem, it is an interesting technique for estimating the instantaneous 'state' of a linear dynamic system perturbed by white -noise measurements that is linearly related to the corrupted white noise state. The resulting estimator is statistically optimal with respect to any quadratic function of the estimation error.

In estimation theory, Kalman introduced stochastic notions that applied to non-stationary time-varying systems, via a recursive solution. C.F. Gauss (1777-1855) first used the Kalman filter, for the least-squares approach in planetary orbit problems. The Kalman filter is the natural extension of the Wiener filter to non-stationary stochastic systems. In contrast, the theory of Kalman has provided optimal solutions for control systems with guaranteed performance. These control analyses were computed by solving formal matrix design equations that generally had unique solutions. By a way of reference, the U.S. space program blossomed with a Kalman filter providing navigational data for the first lunar landing.

Practically, it is one of the celebrated discoveries in the history of statistical estimation theory in the twentieth century. It has enable humankind to do many things, one obvious advantage, is its indispensability as silicon integration in the makeup of electronic systems. It's most dependable application is in the control of complex dynamic systems such as continuous manufacturing processes, aircraft, ships, or spacecraft. To control a dynamic system, you must first know what it is doing. For these applications, it is not always possible or desirable to measure every variable that you want to control, and Kalman filter provides a means of inferring the missing information from indirect (and noisy) measurements. Kalman Filter is also very useful for predicting the likely future course of dynamic systems that people are not likely to control, such as the flow of rivers during flood, the trajectory of celestial bodies, or the prices of traded commodities. Kalman Filter is 'ideally noted for digital computer implementation', arising from a finite representation of the estimated problem-by a finite number of variables. Usually, these variables are assumed to be real numbers-with infinite precision. Some of the problems encountered in its uses, arose from its distinction between 'finite' and 'manageable' problem sizes. These are significant issues on the practical side of Kalman filtering that must be considered in conjunction with the theory. It is also a complete statistical characterization of an estimated problem than an estimator, because it propagates the entire probability distribution of the variables in its task to be estimated. This is a complete characterization of the current state of knowledge of the dynamic system, including influence of all past measurements. These probability distributions are also useful for statistical analysis and predictive design of sensor systems. The applications of Kalman filtering encompass many fields, but its use as a tool, is almost exclusively for two purposes: estimation and performance analysis of estimators. Figure 1 depicts the essential subject for the foundation for Kalman filtering theory.

Despite the indication of Kalman filtering process in the apex of the pyramid, it is an integral part in the foundation of another discipline modern control theory , and a proper subset of statistical decision theory.

Figure 1.

Foundation concept in Kalman filtering.

Kalman filter analyses a dynamic systems' behavior with external and measurement noise. In general, the output y is affected by noise measurement. In addition, the process dynamics are also affected by disturbances, such as atmospheric turbulence. Following this, we shall now present the model for the LQG control for the ELV via equation (1). The essential assumptions are viz; the dynamic system is linear, the performance cost function is quadratic, and the random processes are Gaussian.

By defining, a continuous –time process and measurement model is as follows;

Where, w and v are zero-mean Gaussian noise processes (uncorrelated from each other). The following process and measurement covariance matrices hold namely:

E v ( t ) v T ( s ) = R N δ ( t − s ) E v ( t ) w T ( s ) = 0 E w ( t ) w T ( s ) = Q N δ ( t − s ) } t , s ∈ ℜ

E2

From the foregoing,a Kalman filter equation admits the form;

where L is the Kalman gain represented as

The covariance matrix P, in equation (4) is the solution to a Riccati Differential Equation (RDE) or an Algebraic Riccati Equation (ARE).

Advertisement

3. Riccati equation

In mathematics, a Riccati equation is any ordinary differential equation that is quadratic in the unknown function. In other words, it is an equation of the form

y ′ ( x ) = q 0 ( x ) + q 1 ( x ) y ( x ) + q 2 ( x ) y 2 ( x ) ,

E5

where, q ₀ (x)≠0 and q ₂ (x)≠0 ( q ₀ (x)=0 is Bernoulli equation and q ₂ (x)=0 is first order linear ordinary equation). It is named after Count Jacopo Francesco Riccati (1676-1754).

More generally, "Riccati equations" refer to matrix equations with analogous quadratic terms both in continuous-time and in discrete-time Linear-Quadratic-Gaussian Control. The steady-state (non-dynamic) versions of these equations are classified as algebraic Riccati equations.

3.1. Riccati differential equation (RDE)

The Riccati differential equation was first studied in the eighteen century as a nonlinear scalar differential equation, and a method was derived for transforming it to a linear matrix form. This same method works when the dependent variable of the original Riccati differential equation is a matrix.

The statistical performance of the Kalman filter estimator can be predicted a priori by solving the Riccati equations for computing the optimal feedback gain of the estimator. Also, the behaviors of their solutions can be shown analytically for the most trivial cases. These equations also provide a means for verifying the proper performance of the actual estimator when it is running.

For the LQG problem, the associated Riccati Differential Equation which provides the covariance P(t ) needed for the solution of Kalman gain is of the form,

P ˙ ( t ) = A ϕ ( t ) P ( t ) + P ( t ) A ϕ T ( t ) + G ( t ) Q N ( t ) G ( t ) − P ( t ) C T ( t ) R N − 1 ( t ) C ( t ) P ( t )

E6

where A _ is the state transitional matrix defined as

d d t x ( t ) = A ( t ) x ( t ) + G ( t ) w ( t ) .

E7

The Riccati Differential Equation in (6) can be solved by using a technique, called the Matrix Fraction Decomposition. A matrix product of the sort AB ^-1 is called a matrix fraction, and a representation of a matrix M in the form

A fractional decomposition of the covariance matrix results in a linear differential equation for the numerator and the denominator matrices. The numerator and denominator matrices as functions of time, such that the product A(t)B ^-1 (t) satisfies the matrix Riccati equation and its boundary conditions. By taking the derivative of the matrix fraction A(t)B ^-1 (t) with respect to t and using the fact that

d d t B − 1 ( t ) = − B − 1 ( t ) B ˙ ( t ) B − 1 ( t ) ,

E9

Now let us represent the covariance matrix P(t) by

and on applying equations ( 9-10) yields

d P ( t ) d t = A ˙ ( t ) B − 1 ( t ) − A ( t ) B − 1 ( t ) B ˙ ( t ) B − 1 ( t )

E11

From the Riccati equation in (6) substitution for P(t) with A(t)B ^-1 (t) in the right hand side of the equation, leads to the following namely

d P ( t ) d t = A ϕ ( t ) A ( t ) B − 1 ( t ) + A ( t ) B − 1 ( t ) A ϕ T ( t ) + G ( t ) Q N ( t ) G T ( t )

E12

− A ( t ) B − 1 ( t ) C T ( t ) R N − 1 ( t ) C ( t ) A ( t ) B − 1 ( t ) .

E13

Equating (11) and (12) and multiplying through with B(t) yields

A ˙ ( t ) − A ( t ) B − 1 ( t ) B ˙ ( t ) = { A ϕ ( t ) A ( t ) + G ( t ) Q N ( t ) G T ( t ) B ( t ) }

E14

− A ( t ) B − 1 ( t ) { C T ( t ) R N − 1 ( t ) C ( t ) A ( t ) − A ϕ T ( t ) B ( t ) }

E15

Therefore, if we find A(t) and B(t) that satisfy:

A ˙ ( t ) = A ϕ ( t ) + G ( t ) Q N ( t ) G T ( t ) B ( t ) ,

E16

B ˙ ( t ) = C T ( t ) R N − 1 ( t ) C ( t ) A ( t ) − A ϕ T ( t ) B ( t ) ,

E17

then P(t)=A(t)B ^-1 (t) satisfies the Riccati differential equation. Note that equations (14) and (15) are the linear differential equations with respect to matrices A(t) and B(t) . The foregoing can be arranged as follows viz;

( A ( t ) B ( t ) ) = [ A φ ( t ) G ( t ) Q N ( t ) G T ( t ) C T ( t ) R N − 1 ( t ) C ( t ) − A φ ( t ) ] ( A ( t ) B ( t ) )

E18

Such a representation is a Hamiltonian Matrix known as matrix Riccati differential equation.

Ψ ( t ) = [ A ϕ ( t ) G ( t ) Q N ( t ) G T ( t ) C T ( t ) R N − 1 ( t ) C ( t ) − A ϕ ( t ) ]

E19

The initial values of A(t) and B(t) must be constrained by the initial value of P(t) . This is easily satisfied by taking P ₀ =I , an identity matrix.

In the time-invariant case, the Hamiltonian matrix Ψ is also time-invariant. As a consequence, the solution for the numerator A(t) and denominator B(t) of the matrix fraction can be represented in matrix form as the product

[ A ( t ) B ( t ) ] = e Ψ t [ P ( 0 ) I ] ,

E20

where e ^Ψtis a 2n x 2n matrix.

Convergence Properties of a Scalar Time-Invariant Case. In this case, the numerator A(t) and the denominator B(t) of the 'matrix fraction' A(t)B ^-1 (t) will be scalars, but Ψ will be a 2n x 2n matrix. Considering a case: A(t)→a(t), and B(t)→b(t) and the process and measurement equations becomes

A ϕ ( t ) = A ϕ , G ( t ) = G , Q ( t ) = Q , R ( t ) = R , C ( t ) = C .

E21

The scalar time-invariant Riccati differential matrix equation and its linearized equivalent is

P ˙ ( t ) = A ϕ P ( t ) + P ( t ) A ϕ − P ( t ) C R N − 1 C P ( t ) + G Q G T .

E22

Hence, equation (16) reduces to

( a ˙ b ˙ ) = [ A ϕ G Q G T C R − 1 C − A ϕ ] ( a b )

E23

with the following initial conditions namely; a(0)=P ₀ and b(0)=1 . In the meantime, the eigenvalues of the Hamilton Matrix are;

Using λ ₁ and λ ₂, where, q=G ² Q, we can write the following:

a ( t ) = 1 2 λ { [ P 0 ( λ − A ϕ ) + q ] e λ t + [ P 0 ( λ − A ϕ ) + q ] e − λ t }

E25

b ( t ) = 1 2 λ q { ( λ − A ϕ ) [ P 0 ( λ + A ϕ ) + q ] e λ t − ( λ + A ϕ ) [ P 0 ( λ − A ϕ ) − q ] e − λ t } .

E26

Consequently, the covariance follows as;

P ( t ) = a ( t ) b ( t ) = q [ P 0 ( λ + A ϕ ) + q ] + [ P 0 ( λ − A ϕ ) − q ] e − 2 λ t ( λ − A ϕ ) [ P 0 ( λ + A ϕ ) + q ] − ( λ + A ϕ ) [ P 0 ( λ − A ϕ ) − q ] e − 2 λ t .

E27

If the system is observable , i.e. (A,C) : Observable Pair, then the RDE has a positive-definite, symmetric solution for an arbitrary positive-definite initial value of matrix P ₀ > 0 ;

P ( t ) > 0 p . d . , P ( t ) = P T ( t ) ∈ R n × n , ∀ t > 0.

E28

The need to solve Riccati equation is perhaps the greatest single cause of anxiety and agony on the part of people faced with implementing Kalman filter. Because there is no general formula for solving higher order polynomials equations (i.e., beyond quartic), finding closed-form solutions to algebraic Riccati equations by purely algebraic means is very rigorous. Thus, it is necessary to employ numerical solution methods. Numbers do not always provide us as much insight into the characteristics of the solution as formulas do, but readily amenable for most problems of practical significance.

3.2. Numerical example – An expendable launch vehicle (ELV) autopilot

This problem is taken from Aliyu et al, and it is significant for modeling and simulating an ELV autopilot problem in Matlab/Simulink^®. It solves the symmetrical RDE:

P ˙ ( t ) − A P ( t ) + P ( t ) A − P ( t ) C R N − 1 C P ( t ) + G Q N G T , P 0 = I .

E29

Where,

A = [ 0 1 0 14.7805 0 0.01958 − 100.858 0 − 0.1256 ] , Q N = [ 1.1 × 10 − 3 0 0 0 1.1 × 10 − 3 0 0 0 1.1 × 10 − 3 ] ,

E30

R N = [ 4.0 × 10 − 6 0 0 0 4.0 × 10 − 6 0 0 0 4.0 × 10 − 6 ] , C = [ 1 0 0 0 1 0 0 0 0 ] ,

E31

and

G = [ 0 14.7805 − 94.8557 ] T .

E32

3.3. Numerical Methods and Problem Solving Environment (PSE), for Ordinary Differential Equations

In the last decade, two distinct directions have emerged in the way Ordinary Differential Equation (ODE) solvers software is utilized. These include Large Scale Scientific Computation and PSE. Most practicing engineers and scientists, as well as engineering and science students use numerical software for problem solving, while only a few very specific research applications require large scale computing.

MATLAB^® provides several powerful approaches to integrate sets of initial value, Ordinary Differential Equations. We have carried out an extensive study of the requirements. For the simulation of the autopilot problem, we have used the mathematical development environment Matlab/Simulink^®. Matlab/Simulink^® was chosen, as it is widely used in the field of numerical mathematics and supports solving initial value ordinary differential equations like the type we have in (27) with easy.

From the humble beginnings of Euler's method, numerical solvers started relatively simple and have evolved into the more complex higher order Taylor methods and into the efficient Runge-Kutta methods. And the search for more efficient and accurate methods has led to the more complicated variable step solvers.

3.3.1. One step solver

For solving an initial value problem

a numerical method is needed. One step solvers are defined by a function Ф(x,y,h;f) which gives approximate values y _i ≔y(x _i ) for the exact solution y(x) :

y i + 1 : = y i + h Φ ( x i , y i , h ; f ) ,

E34

where, h denotes the step size. In the following let x and y be arbitrary but fixed, and z(t) is the exact solution of the initial value problem

z ′ ( t ) = f ( t , z ( t ) ) , z ( x ) = y

E36

with the initial values x and y . Then the function

Δ ( x , y , h , f ) : = { z ( x + h ) − y h h ≠ 0 f ( x , y ) h = 0

E37

describes the differential quotient of the exact solution z(t) with step size h , whereas Ф(x,y,h;f) is the differential quotient of the approximated solution with step size h . The difference  = ∆ - Ф is the measure of quality of the approximation method and is denoted as local discretization error.

In the following, F _N (a,b) is defined as the set of all functions f , for which exist all partial derivations of order N on the area

S = { x , y | a ≤ x ≤ b , y ∈ ℜ n } a , b finite,

E38

where they are continuous and limited.

One step solvers must fulfill

This is equivalent to

lim h → 0 Φ ( x , y , h ; f ) = f ( x , y ) .

E40

If this condition holds for all x є [a,b], y є F ₁ (a,b) then Ф and the corresponding one step method are called consistent. Thus, the one step method is of order p , if

holds for all x є [a,b], y є R, f є F_p (a,b). The global discretization error

e n ( X ) : = y ( X ) − y n X = x n fix, n variable

E42

is the difference between exact solution and the approximated solution. The one step method is denoted as convergent , if:

Theorem: Methods of order p > 0 are convergent and it holds

This means that the order of the global discretization error is equal to the order of the local discretization error. The crucial problem concerning one-step methods is the choice of the step size h . If the step size is too small, the computational effort of the method is unnecessary high, but if the step size is too large, the global discretization error increases. For initial values x ₀ ,y ₀ a step size as large as possible would be chosen, so that the global discretization error is below a boundary ε after each step. Therefore, a step size control is necessary.

3.3.2. Explicit Euler

The most elementary method of solving initial value problems is the explicit Euler. The value of y _i+1 can be calculated the following way:

The explicit Euler calculates the new value y _i+1 by following the tangent at the old value for a distance of h . The slope of the tangent is given by the value of f (x _i ,y _i ) . The explicit Euler uses no step size control; the step size h is fixed. Therefore, it is only useful in special cases, where the function to integrate is pretty flat. Nevertheless, it is very easy to implement and calculates very fast, so it can be a good choice.

3.3.3. Runge-Kutta method

The Runge-Kutta methods are a special kind of one-step solvers, which evaluate the right side in each step several times. The intermediate results are combined linearly. The general discretization schema for one-step of a Runge-Kutta method is

y 1 = y 0 + h ( b 1 K 1 + b 2 K 2 + ⋯ + b a K a ) ,

E46

with corrections

K i = f ( x 0 + c i h , y 0 + h ∑ j = 1 i − 1 a i j K j ) , i = 1 , ⋯ s .

E47

The coefficients are summarized in a tableau, the so-called Butcher-tableau, see figure 2.

Figure 2.

Butcher-tableau.

3.4. Step size control

The Runge-Kutta methods use an equidistant grid, but this is for most applications inefficient. A better solution is to use an adaptive step size control. The grid has to be chosen so that

• a given accuracy of the numerical solution is reached

• the needed computational effort is minimized.

As the characteristics of the solution are a priori unknown, a good grid structure cannot be chosen before the numerical integration. Instead, the grid points have to be adapted during the computation of the solution. Trying to apply this to Runge-Kutta methods lead to the following technique:

To create a method of order p (for y _i+1), it is combined with a method of order P+1 (for ŷ _k+1).

This method for y _i+1 is called the embedded method. The idea of embedding was developed by Fehlberg and methods using this technique therefore are called Runge-Kutta-Fehlberg methods. This leads to a modified Butcher-tableau (see figure 3). The new step size is calculated with

where ε denotes the tolerance.

Figure 3.

Modified Butcher-tableau for embedded Runge-Kutta-methods.

3.4.1. Error control and variable step size

The main concern with numerical solvers is the error made when they approximate a solution. The second concern is the number of computations that must be performed. Both of these can be addressed by creating solvers that use a variable step size in order to keep the error within a specified tolerance. By using the largest step size allowable while keeping the error within a tolerance, the error made is reduced.

The way to keep the error under control is to determine the error made at each step. A common way to do this is to use two solvers of orders p and p+1 , as earlier explained. Any approximations made of order p will have an error no larger than the value of the p + 1 term. This leads us to take the difference of the two solvers to find the value of the error term.

Since the downside of using two distinct methods is a dramatic increase in computations, another method is typically used. An example of this method is the Rung-Kutta-Fehlberg Algorithm. The Rung-Kutta-Fehlberg combines Rung-Kutta methods of order four and order five into one algorithm. Doing this reduces the number of computations made while returning the same result.

3.4.2. Dormand-Prince method

The Dormand-Prince method is a member of the Runge-Kutta-Fehlberg class with order 4(5).It means that the method has order 5 and the embedded method has order 4. This is described by the following equations:

y ( x 0 + h ) = y 0 + h ∑ k = 0 4 b k f k ( x 0 , y 0 ; h ) y ^ ( x 0 + h ) = y 0 + h ∑ k = 0 5 b ^ k f k ( x 0 , y 0 ; h ) f k = f ( x 0 + c k h , y 0 + h ∑ t = 0 k − 1 a k i f i )

E49

The coefficients from Dormand and Prince can be seen in figure 4.

Figure 4.

Butcher-tableau for Dormand-Prince-method.

For solving an initial value problem like the one we have in (27) Matlab was chosen, as it is widely used in the field of numerical mathematics and supports solving ordinary differential equations. Moreover, it is possible to visualize the simulation results of the autopilot. In our program we used the ode45 , a standard solver included in Matlab/Simulink. The solver ode45 implements the method of Dormand-Prince , which is a member of the class of Runge-Kutta-Fehlberg methods. More specifically, the Dormand–Prince method uses six function evaluations to calculate fourth- and fifth-order accurate solutions. The difference between these solutions is then taken to be the error of the (fourth-order) solution. This error estimate is very convenient for adaptive step size integration algorithms. This adaptive step-size control algorithm monitors the estimate of the integration error, and reduces or increases the step size of the integration in order to keep the error below a specified threshold. The accuracy requested is that both the relative and absolute (maximal) errors be less than the truncation error tolerance. In MATLAB, both relative ( RelTol ) and absolute ( AbsTol ) tolerances can be specified. The default values (that were used in solving the problem) are RelTol = 0.001 and AbsTol = 10^-6.We intend to integrate the DRE from t=0 up to t=1. The Simulink model for the DRE is as shown in Figure 5.

Figure 5.

Simulink model for matrix Differential Riccati Equation.

After successfully simulating the above model, it was used to design an Linear Quadratic Gaussian (LQG) autopilot with the following Linear Quadratic Regulator (LQR) Characteristics;

Q = [ 2.5 0 0 0 4 0 0 0 173.6 ] , and R = 0.1.

E50

For this autopilot, the Kalman-Bucy filter model was implemented as shown in Fig.6. It should be noted that if for any reason the initial condition P₀ in (27) is taking as a matrix with entries less than 1, then initial covariance matrix could be used as a tuning parameter to meet a specific time response characteristics as was presented in Aliyu, et al.

Advertisement

4. Filter performance

The dependent variable in the Riccati differential equation of the Kalman-Bucy filter is the covariance matrix of the estimation error, defined as the difference between the estimated state vector x-hat and the true state vector x . Matrix P is a matrix of covariance of an error estimate of the state vector x . The initial value of which is chosen as

P 0 = E { [ x ( t ) − x ^ ( t ) ] [ x ( t ) − x ^ ( t ) ] T } At t → ∞ .

E51

The state error covariance matrix is n × n and symmetric, and must remain positive definite to retain filter stability. Diagonal elements of this matrix are variances of errors of the estimations for corresponding components of the state vector. These also serve as a definition of accuracy for the estimation.

Figure 6.

Simulink model for Kalman-Bucy filter with a RDE.

The solution of the matrix Riccati equation was found to provide a quantitative measure of how well the state variables can be estimated in terms of mean-squared estimation errors. Therefore, the matrix Riccati equation from the Kalman filter was soon recognized as a practical model for predicting the performance of sensor systems, and it became the standard model for designing aerospace sensor systems to meet specified performance requirements. More importantly, covariance analysis is crucial in exploring what-if scenarios with new measurement sources.

Note that in (27) we increase estimation uncertainty by adding in process noise and we decrease estimation uncertainty by the amount of information ( R^-1 ) inherent in the measurement.

For an initial guess for the value of covariance, a very large value could be selected if one is using a very poor sensor for measurement. This makes the filter very conservative. Converse is the case if very good sensors are used for measurement.

The LQG autopilot simulation for tracking a pitch angle of 3 degrees (0.05rads) with the observer as designed in Fig.6 gave the result presented in Fig.7. It is interesting to note that the time response characteristics of the simulated autopilot in Fig. 7 meets all the design specifications of; percentage overshoot less than 10 percent; settling time of less than 4 seconds; rise time of less than 1 second and steady state error of less than 2 percent.

Figure 7.

Set-point command tracking of LQG autopilot for a RDE solution to Kalman gain.

The numerical result at t=1 for the covariance matrix with respect to Fig.5 is given in (47) and hence the associated Kalman gain is given in (48). The Kalman gain harnessed at this point urged us to re-design the Kalman filter model as shown in Fig. 8 for our LQG autopilot.

P = [ 5.228197174 × 10 − 6 4.261615461 × 10 − 6 − 0.000394471297 4.261615461 × 10 − 6 0.0009807093782 0.0006722035747 − 0.0003944771297 0.0006722035747 8.750905161 ] ,

E52

L = [ 1.30704929362596 1.06540386549228 0 1.06540386549228 245.177344558508 0 − 98.6192824463156 168.050893692856 0 ] .

E53

A further investigation was carried out-the single point value of Kalman filter gain given in (48) was used to implement the Kalman filter algorithm as popular represented in most textbooks-as a constant gain. For which, the Kalman-Bucy model in Fig. 8 was developed.

Figure 8.

Simulink Model of Kalman filter model for a constant gain value of Kalman gain.

Hence, the same LQG autopilot was simulated with the Kalman filter based observer as shown in Fig.8. Simulation result for the system is as shown in Fig. 9. It is also interesting to note that all the time response characteristics as earlier mentioned were met. Though, the LQR controller could bring the ELV to a settling time at about 2 seconds.

The Matlab in-built command function [K,P,E]=lqr(A,B,C,D,Q,R) was used to obtain the solution for the design of the LQR controller. Where, K is the controller gain, P is the associated solution to the Algebraic Riccati Equation of the controller design and E , the closed-loop eigenvalues of the plant dynamics. Note, that for LQR design the pair (A,B) must be controllable then, a state feedback control law can be constructed to arbitrarily locate the closed-loop eigenvalues.

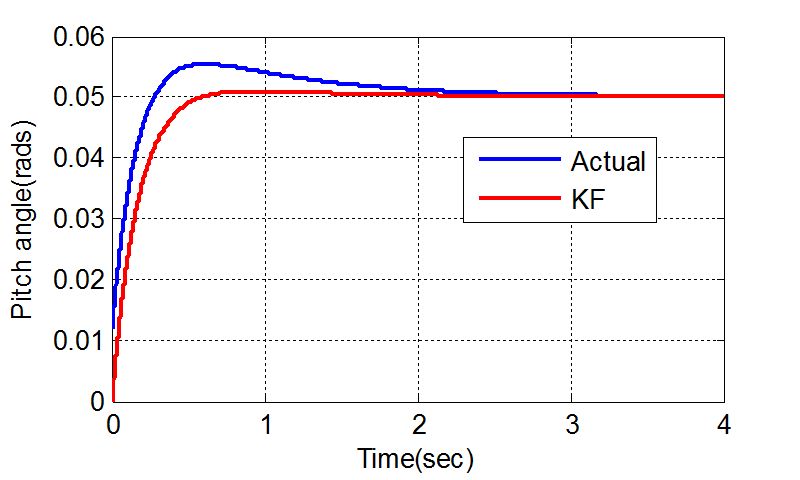
Figure 9.

Set point command tracking of ELV autopilot for a Kalman gain obtained by evaluating covariance matrix to a Riccati Differential Equation at t=1sec.

Advertisement

5. Algebraic Riccati equation

Assume that the Riccati differential equation has an asymptotically stable solution for P(t):

Then the time derivative vanishes

Substituting this into the (6) yields

A P + P A T + G Q G T − P C T R − 1 C P = 0.

E56

This is called the Algebraic Riccati Equation. This is a nonlinear matrix equation, and need a numerical solver to obtain a solution for P_∞.

Consider a scalar case: P _∞ є R^1×I, A_,C, Q, R,G є R^1×I. The Algebraic Riccati Equation can be solved analytically

P ∞ = R C 2 { A ϕ ± A ϕ 2 + Q R C 2 G 2 } .

E58

From (52) there exist two solutions; one positive and the other negative, corresponding to the two values for the signum (±). There is no cause for alarm. The solution that agrees with (52) is the non-negative one. The other solution is non-positive. We are only interested in the non-negative solution, because the variance P of uncertainty is, by definition, non-negative. Thus, taking the positive solution

lim t → ∞ P ( t ) = P ∞ = R C 2 { A ϕ + A ϕ 2 + Q R C 2 G 2 }

E59

For the numerical example at hand, the Kalman gain for this problem is easily solved with the following Matlab command [L, P,E]=lqe(A,G,C,Q,R) . This command solves a continuous time Algebraic Riccati Equation associated with the described model. Where, L, is the Kalman gain, P , the covariance matrix, and E , the closed-loop eigenvalues of the observer. The numeric values are as follows respectively:

L = [ 0.999999834557877 1.0005722536001 0 1.00057522536001 23530.07308334456 0 − 12.5039701153711 − 150868.724947992 0 ] ,

E60

P = [ 3.99999938 × 10 − 6 4.0023 × 10 − 6 − 5.0016 × 10 − 5 4.0023 × 10 − 6 0.0941 × 10 − 6 − 0.6035 − 5.0016 × 10 − 6 − 0.6035 673.4535 ] ,

E61

and

E = [ − 23530.19862489 − 1.00000017144017 − 5.81187094955956 × 10 − 5 ] .

E62

Based, on the result in (54), the LQG autopilot was simulated with the Kalman-Bucy filter state observer as modeled in Fig. 8. The result obtained from this was used in designing an LQG controller for the case of an ELV during atmospheric ascent. This seeks to track and control a pitch angle of 3 degrees (0.05rads) and the result is as shown Figure 10. Though, in this case the controller could bring the ELV to a Settling Time at 3 seconds. A minute further, compared to that obtained in Fig. 9. In both cases a negligible difference in Percentage Overshoot was observed.

Figure 10.

Set-point command tracking of LQG autopilot for an Algebraic Riccati Equation's solution to Kalman gain.

Advertisement

6. Comparative analysis

It can be clearly seen from figure 7 that the result of applying Kalman gain in the LQG problem of an ELV is most suitable by solving the associated Riccati Equation in its differential form (RDE). All time response characteristics were met within a second and with a zero percent overshoot ! Though, issues might arise when hardware implementation is to be carried out. This basically will be due to the computational demand that will be placed on the selected micro-controller. In view of that, if we choose to design the Kalman filter in the traditional manner but still not solving the associated Riccati equation as an algebraic one but as a differential one as done earlier and then harvesting the value of the Kalman gain at some specific point (in this research, we chose 1 second). Then, applying the Kalman gain, as a constant gain throughout the regime of simulation (RDE@1sec). It is obvious that for this example, this result still out performs that obtained from solving an Algebraic Riccati Equation (ARE). Actually, it could be clearly seen in Fig. 9 that the settling time is 2 second and in Fig. 10 is 3 seconds as the case applies. Figure 11 tries to give a holistic view of the three cases considered in this research for perusal.

Though one might be tempted to look at the difference in settling time of 1 second between the case of harvesting the Kalman gain value after solving a RDE at t=1sec., With that of ARE as negligible or insignificant. On the contrary, considering an aerospace vehicle like the ELV, moving with a speed rage of Mach number 0.8-1.2 (transonic). One will be force to rethink. Let alone, compared to a settling time of 0.7sec obtained when Kalman gain is obtained from solving a RDE.

It is of paramount interest to add here that the plant and observer dynamics for all cases explored in this research gave a dynamic system with stable poles ( separation principle ). Contrary to that obtained in the paper Aliyu et al and in the book Aliyu Bhar Kisabo.

Figure 11.

Compared results of the three approaches to the solution of Kalman gain as applied to an autopilot.

Advertisement

7. Conclusion

It can be clearly seen in Figure 6, that the synthesized LQG autopilot, with Kalman gain obtained by solving an Algebraic Riccati Equation (ARE) has 6 percent overshoot and a settling time of 3seconds. While, that in Fig. 3, is most preferred in all time-domain characteristics-zero percentage overshoot and settling time of 0.7second. This is the result of implementing Kalman gain as a solution to a Riccati Differential Equation (RDE). Thus, the solution to Riccati Differential Equation for the implementation of Kalman filter in LQG controller design is the most optimal for pitch plane control of an ELV in the boast phase.

It is required that after designing Kalman filter, the accuracy of estimation is also assessed from the covariance matrix. It could be seen that both cases gave a very good estimation (very small covariance). Though, that of ARE gave a much smaller value. This has less significance to our research since we are majorly interested in the time response characteristic of the controlled plant. MATLAB 2010a was used for all the simulations in this paper.

Advertisement

Acknowledgement

The authors will like to specially appreciate the Honourable Minister of Science and Technology, Prof. Ita Okon Bassey Ewe, for his special intereste in the Research and Development activities at National Space Research and Development Agency (NASRDA). His support has been invaluable. Also, in appreciation is the Director-General of NASRDA, Dr. S. O Mohammed for making CSTP a priority agency among others Centres of NASRDA. We also thank Dr. Femi A. Agboola, Director , Engineering and Space Systems (ESS) at NASRDA, for his meaningful suggestions and discussions.

References

1. 1. Aliyu Bhar Kisabo. 2011Expendable Launch Vehicle Flight Control; Design & Simulation With Matlab/Simulink, 973-3-84432-729-8Germany.
2. 2. Shampine L. F. Gladwell I. Thompson S. 2003Solving ODEs with MATLAB, 978-0-51107-707-4USA.
3. 3. Robert H. Bishop 2002The mechatronics Handbook, Second Edition, 0-84930-066-5Raton, London, New York, Washington D.C
4. 4. Mohinder S. Grewal Angus P. Anderson 2001Applications of kalman Filtering; Theory & practice Using Matlab, Second Edition, 0-47126-638-8York, Chichester, Weinhem, Brisban,Sigapore,Toronto
5. 5. Aliyu Bhar Kisabo et al 2011Autopilot Design for a Generic Based Expendable Launch Vehicle, Using Linear Quadratic gaussian (LQG) Control. European Journal of Scientific Research, 50 4February 2011), 597 611 0145-0216X
6. 6. Reza Abazari. 2009Solution of Riccati Type Differential Equations Using Matrix Differential Transform. Journal of Applied Mathematics & Informatics, 27 5-6December 2009), 1133 1143

Written By

Bhar K. Aliyu, Charles A. Osheku, Lanre M.A. Adetoro and Aliyu A. Funmilayo

Submitted: December 5th, 2011 Published: September 26th, 2012

© 2012 The Author(s). Licensee IntechOpen. This chapter is distributed under the terms of the Creative Commons Attribution 3.0 License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

daletionve84.blogspot.com

Source: https://www.intechopen.com/chapters/39345